Thi hc kì 2 là bài kim tra kin thc ánh giá quá trình hc tp trong hc kì th hai ca nm hc. t kt qu tt nht, các em cn ôn thI hc kì 2 úng trng tâm bài hc. Chính vì vy, VUIHOC ã tng hp kin thc ôn thi hc kì 2 lp 10 môn toán giúp các em ôn thi d dàng hn.

1. cng ôn thi hc kì 2 lp 10 môn toán: i s t hp
1.1 Quy tc m, cng và nhân
a. Quy tc m:
- Vi các s cách u nhau ta có:
S các s = ( s ln nht - s nh nht): khong cách gia 2 s lin k + 1
- Du hiu chia ht:
-
Chia ht cho 2: S có ch s tn cùng là 0,2,4,6,8.
-
Chia ht cho 3: Tng các ch s chia ht cho 3.
-
Chia ht cho 4: Hai ch s tn cùng lp thành s chia ht cho 4.
-
Chia ht cho 5: S có ch s tn cùng là 0,5.
-
Chia ht cho 6: S chi ht cho 2 và 3.
-
Chia ht cho 8: S có 3 ch s tn cùng lp thành s chia ht cho 8.
-
Chia ht cho 9: S có tng các ch s chia ht cho 9.
b. Quy tc cng:
- Nu mt quá trình (bài toán) có th thc hin c mt trong hai cách (trng hp) loi tr ln nhau: cách th nht cho m kt qu và cách th hai cho n kt qu. Khi ó vic thc hin quá trình trên cho m + n kt qu.
- Nu mt quá trình (bài toán) có th thc hin c k cách (trng hp) loi tr ln nhau: cách th nht cho m1 kt qu, cách th hai cho m2 kt qu, …, cách th k cho mk kt qu. Khi ó vic thc hin quá trình trên cho m1 + m2 + … + mk kt qu.
c. Quy tc nhân:
- Nu mt quá trình (bài toán) ñc thc hin theo hai giai on (bc) liên tip nhau sao cho có m cách thc hin giai on th nht, ng thi ng vi mi cách ó có n cách thc hin giai on th hai. Khi ó có m.n cách thc hin quá trình trên.
- Nu mt quá trình (bài toán) c thc hin theo k giai on (bc) liên tip nhau sao cho có m1 cách thc hin giai on th nht, vi mi cách ó có m2 cách thc hin giai on th hai, …, có mk cách thc hin giai on th k. Khi ó, toàn b quá trình có m1.m2…mk cách thc hin.
1.2 Hoán v, chnh hp và t hp
a. Hoán v: Cho tp hp X gm n phn t phân bit (n  0). Mi cách sp xp n phn t ca X theo mt th t nào ó c gi là mt hoán v ca n phn t. S các hoán v ca n phn t c ký hiu là Pn.
0). Mi cách sp xp n phn t ca X theo mt th t nào ó c gi là mt hoán v ca n phn t. S các hoán v ca n phn t c ký hiu là Pn.
Pn = n! = 1.2...n (Quy c: 0! = 1)
b. Chnh hp: Cho tp hp X gm n phn t phân bit (n 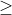 0 ). Mi cách chn ra k (0
0 ). Mi cách chn ra k (0 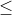 k
k 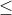 n) phn t ca X và sp xp theo mt th t nào ó c gi là mt chnh hp chp k ca n phn t. S các chnh hp chp k ca n phn t c ký hiu là
n) phn t ca X và sp xp theo mt th t nào ó c gi là mt chnh hp chp k ca n phn t. S các chnh hp chp k ca n phn t c ký hiu là 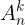
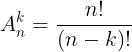
Nhn xét: 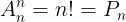
c. T hp: Cho tp hp X gm n phn t phân bit (n 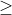 0 ). Mi cách chn ra k (0
0 ). Mi cách chn ra k (0 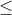 k
k 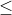 n) phn t ca X c gi là mt t hp chp k ca n phn t. S các t hp chp k ca n phn t c ký hiu là
n) phn t ca X c gi là mt t hp chp k ca n phn t. S các t hp chp k ca n phn t c ký hiu là 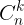
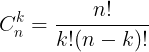
1.3 Nh thc Newton
a. nh ngha: Nh thc newton là khai trin tng ly tha có dng:
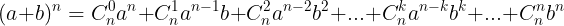
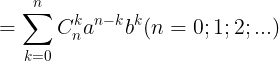
+ S hng th k + 1 là  thng c gi là s hng tng quát.
thng c gi là s hng tng quát.
+ Các h s 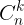 c tính theo công thc t hp hoc da vào tam giác pascal.
c tính theo công thc t hp hoc da vào tam giác pascal.

b. Tính cht:
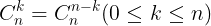
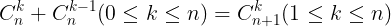
c. Khai trin nh thc newton:
- Dng khai trin: ( a + b)n hoc (a - b)n
- Dng o hàm:
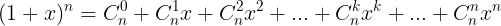
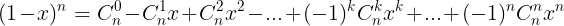
- Dng tích phân:

2. cng ôn thi hc kì 2 lp 10 môn toán: Mt s yu t thng kê và xác sut
2.1 S gn úng và sai s
- Trong nhiu trng hp ta không tìm c s úng mà ch tìm c giá tr xp x ca nó. Giá tr này c gi là s gn úng và c kí hiu là a.
- S gn úng và s úng có s sai lch mt i lng nht nh. ánh giá sai lch ó ta s dng khái nim sai s tuyt i ca s gn úng a, c kí hiu là 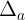 , khi ó
, khi ó 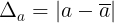 . Trong thc t, ôi khi ta không bit giá tr ca s úng nên không th tính c sai s tuyt i. Ta ch có th ánh giá
. Trong thc t, ôi khi ta không bit giá tr ca s úng nên không th tính c sai s tuyt i. Ta ch có th ánh giá 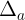 không vt quá mt s d nào ó. Nu
không vt quá mt s d nào ó. Nu 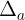
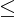 d thì a - d
d thì a - d 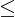
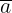
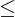 a +d, khi ó ta vit
a +d, khi ó ta vit 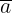 = a
= a 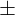 d.
d.
- Sai s tng i ca s gn úng a c kí hiu là 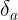 là t s gia sai s tuyt i và |a|
là t s gia sai s tuyt i và |a|
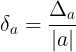
- Nu 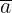 a
a 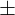 d thì
d thì 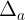
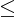 d =>
d => 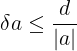 vì vy
vì vy 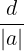 càng nh thì cht lng ca phép o càng cao.
càng nh thì cht lng ca phép o càng cao.
2.2 S quy tròn
- S quy tròn là s thu c sau khi thc hin làm tròn s, s quy tròn gn úng s ban u.
- Quy tc:
+ S ngay sau hàng quy tròn nh hn 5 thì ch cn thay ch s ó và các ch s bên phi bi s 0.
+ S ngay sau hàng quy tròn ln hn 5 thì ta thay ch s ó và các ch s bên phi nó bi 0 và cng thêm 1 n v và s hàng làm tròn.
3. cng ôn thi hc kì 2 lp 10 môn toán: Phng pháp ta trong mt phng
3.1 Phng trình ng thng
a. Véc t ch phng ca ng thng:
- Véc t 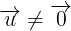 c gi là véc t ch phng ca ng thng
c gi là véc t ch phng ca ng thng 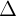 nu giá ca nó song song hoc trùng vi
nu giá ca nó song song hoc trùng vi 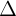
- Nu 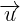 là mt véc t ch phng ca
là mt véc t ch phng ca 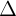 thì k
thì k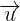 (k
(k 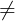 0) cng là véc t ch phng ca
0) cng là véc t ch phng ca 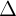 .
.
- Mt ng thng có th xác nh nu bit mt im và mt véc t ch phng.
b. Véc t pháp tuyn ca ng thng
- Véc t 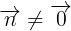 c gi là véc t pháp tuyn ca ng thng
c gi là véc t pháp tuyn ca ng thng 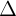 nu giá ca nó vuông góc vi
nu giá ca nó vuông góc vi 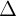 .
.
- Nu 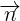 là mt véc t pháp tuyn ca
là mt véc t pháp tuyn ca 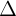 thì k
thì k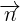 (k
(k 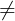 0) cng là véc t pháp tuyn ca
0) cng là véc t pháp tuyn ca  .
.
- Mt ng thng có th xác nh nu bit mt im và véc t pháp tuyn.
- Véc t pháp tuyn vuông góc vi véc t ch phng.
c. Phng trình ng thng
- Cho ng thng 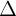 i qua Mo(xo;yo) và có véc t ch phng
i qua Mo(xo;yo) và có véc t ch phng 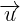 = (u1;u2)
= (u1;u2)
+ Phng trình tham s ca 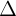 :
:
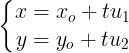
+ Phng trình chính tc ca 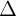 :
:
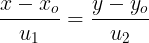
+ Phng trình tng quát ca ng thng: 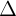 : ax + by + c = 0 , trong ó:
: ax + by + c = 0 , trong ó:
+ Mt s trng hp c bit:
| Các h s | Phng tình ng thng 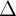 | Tính cht ng thng 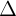 |
| a = 0 | by + c = 0 | 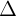 // Ox hoc // Ox hoc 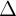 trùng Ox trùng Ox
|
| b = 0 | ax + c = 0 | 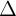 // Oy hoc // Oy hoc 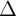 trùng Oy trùng Oy
|
| c = 0 | ax + by = 0 |  i qua gc ta O i qua gc ta O
|
d. V trí tng i ca hai ng thng
- Cho hai ng thng 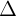 1: a1x + b1y + c1 = 0 và
1: a1x + b1y + c1 = 0 và 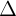 2: a2x + b2y + c2 = 0
2: a2x + b2y + c2 = 0
- Ta giao im ca 2 ng thng trên là nghim ca h phng trình:
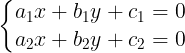 (1)
(1)
+ Nu 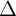 1 ct
1 ct 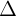 2 thì h (1) có 1 nghim
2 thì h (1) có 1 nghim
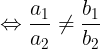 ( nu a2 , b2, c2)
( nu a2 , b2, c2)
+ Nu 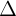 1 //
1 // 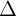 2 thì h (1) vô nghim
2 thì h (1) vô nghim
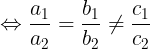 ( nu a2 , b2, c2)
( nu a2 , b2, c2)
+ Nu  1 trùng
1 trùng 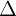 2 thì h (1) có vô s nghim
2 thì h (1) có vô s nghim
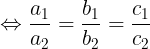 ( nu a2 , b2, c2)
( nu a2 , b2, c2)
e. Góc gia hai ng thng:
- Cho hai ng thng 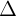 1: a1x + b1y + c1 = 0 có
1: a1x + b1y + c1 = 0 có 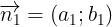 và
và 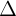 2: a2x + b2y + c2 = 0 có
2: a2x + b2y + c2 = 0 có 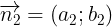
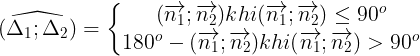
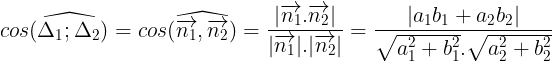
- Chú ý:
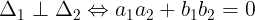
Cho 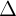 1: y = k1x + m1 ;
1: y = k1x + m1 ; 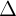 2 = k2x + m2 = 0:
2 = k2x + m2 = 0:
+ Nu 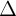 1 //
1 // 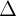 2
2 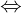 k1 = k2
k1 = k2
+ Nu 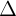 1
1 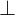
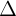 2
2 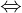 k1.k2 = -1
k1.k2 = -1
f. Khong cách t mt im n mt ng thng:
- Cho ng thng  : ax + by + c = 0 và im Mo(xo;yo)
: ax + by + c = 0 và im Mo(xo;yo)
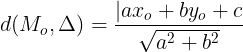
- V trí tng i ca hai im i vi mt ng thng:
+ Cho ng thng  : ax + by + c = 0 và im M(xM;yM) ; im N(xN; yN) không thuc
: ax + by + c = 0 và im M(xM;yM) ; im N(xN; yN) không thuc  .
.
- Phng trình các ng phân giác ca các góc to bi hai ng thng:
+ Cho hai ng thng  1: a1x + b1y + c1 = 0 và
1: a1x + b1y + c1 = 0 và  2: a2x + b2y + c2 = 0 ct nhau. Phng trình ng phân giác ca các góc to bi hai ng thng
2: a2x + b2y + c2 = 0 ct nhau. Phng trình ng phân giác ca các góc to bi hai ng thng  1 và
1 và  2 là:
2 là:
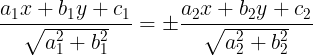
3.2 Phng trình ng tròn
a. Phng trình ng tròn có tâm I(a;b) và bán kính R:
(x - a)2 + (y - b)2 = R2
b. Phng trình tip tuyn ca ng tròn:
Cho ng tròn (C) có tâm I và bán kính R và ng thng 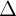 . ng thng
. ng thng 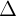 tip xúc vi (C) khi: d(I,
tip xúc vi (C) khi: d(I,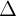 ) = R.
) = R.
3.3 Phng trình ng hypebol:
a. nh ngha:
- Cho F1, F2 c nh vi F1F2 = 2c (c > 0)
M 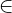 (H)
(H)  |MF1 - MF2| = 2a (a > c)
|MF1 - MF2| = 2a (a > c)
b. Phng trình chính tc:
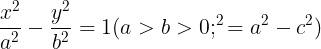
- Ta các tiêu im: F1(-c;0) ; F2(c;0)
3.4 Phng trình ng elip:
a. nh ngha:
Cho F1, F2 c nh vi F1F2 = 2c (c > 0)
M 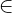 (E)
(E)  MF1 + MF2 = 2a (a > c)
MF1 + MF2 = 2a (a > c)
b. Phng trình chính tc:
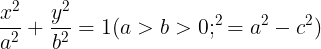
- Ta các tiêu im: F1(-c;0) ; F2(c;0)
4. cng ôn thi hc kì 2 lp 10 môn toán: Luyn tp
Bài 1:
a) Khai trin biu thc (3x + 1)5 . Tìm h s ca x4 trong khai trin (3x+1)5
b) Bit rng trong khai trin (ax + 1/4)4 s hng không cha x là 24. Hãy ca tham s a.
Li gii:
a. 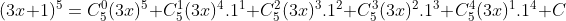
= 1.243x5 + 5.81x4.1 + 10.27x3.1+10.9.x2.1 + 5.3x.1 + 1.1
= 243x5 + 405x4 + 270x3 + 90x2 + 15x + 1
Vy h s x4 trong khai trin trên là 405.
b. Cho (ax + 1/4)4
S hng tng quát:
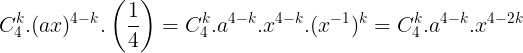
Theo bài s hng không cha x có h s là 24 vy s hng ó tng ng vi:
4 - 2k = 0 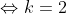
Vy 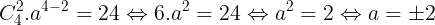
Bài 2:
Mt hp cha 6 qu cu và 4 qu cu vàng, ly ra ngu nhiên cùng mt lúc 4 qu. Tính xác sut ca các bin c sau.
a) A: “Bn qu ly ra cùng màu”
b) B: “ Có ít nht mt qu ”
Li gii: Ta có 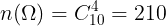
a. Ly ra 4 qu màu : 
Ly ra 4 qu màu vàng: 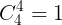
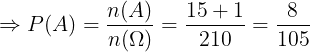
b. Có ít nht 1 qu :
Vy 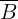 :"Bn qu không (tc bn qu vàng):
:"Bn qu không (tc bn qu vàng): 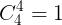
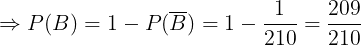
Bài 3:
Cho 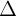 ABC vi A(1;4), B(3;-1) và C(6;7). Vit phng trình tng quát ca ng cao k t A ca
ABC vi A(1;4), B(3;-1) và C(6;7). Vit phng trình tng quát ca ng cao k t A ca  ABC.
ABC.
Li gii:
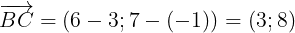
ng thng BC i qua B(-3;-1) nhn 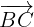 là VTCP
là VTCP
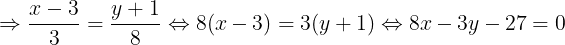
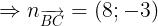
ng cao k t A i qua A(1;4) nhn 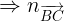 là VTCP
là VTCP
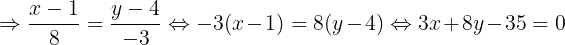
Vy phng trình tng quát ca ng cao k t A ca  ABC là
ABC là 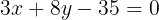
Bài 4:
a. Tìm ta các tiêu im, ta các nh ca elip sau:
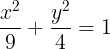
b. Vit phng trình chính tc ca elip bit dài trc ln là 20, tiêu c là 12.
Li gii:
a. 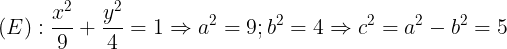
Vy elip có 2 tiêu im 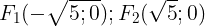
Elip có 4 nh A1(-3;0) ; A2(3;0) ; B1(-2;0) ; B2(2;0)
b. Gi 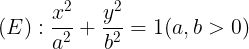
dài trc ln là 20 => 2a = 20 => a = 10.
Tiêu c là 12 => 2c = 12 => c = 6
=> b2 = a2 - c2 = 100 - 36 = 64
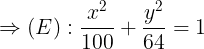
Trên ây là nhng kin thc trng tâm ôn thi hc kì 2 lp 10 môn toán mà VUIHOC ã tng hp da trên các bài hc trong chng trình toán 10. làm tt bài thi gia k, các em cn ghi nh và nm chc c các kin thc và cách gii dng dng bài tp liên quan n kin thc ó. Chúc các em làm tt và t im cao môn Toán trong bài thi hc kì 2 nhé!
Ngun:
https://vuihoc.vn/tin/thpt-de-cuong-on-thi-hoc-ki-2-lop-10-mon-toan-chi-tiet-2993.html
文章定位:





