UNITY: Game Development Tool License Comparisons
这是一个创建于 1393 天前的主题,其中的信息可能已经有所发展或是发生改变。
标准 XYZ 空间,只知道直线的旋转角度,怎么求方向向量?
比如旋转角度为:
(30, 30, 30) 工作几年后这些东西全忘了,也不知道该发哪,作业帮么……
有会的朋友指点一下吧,谢谢
第 1 条附言 2022-02-23 23:58:45 +08:00
是指绕 xyz 轴旋转,演示软件为 Blender 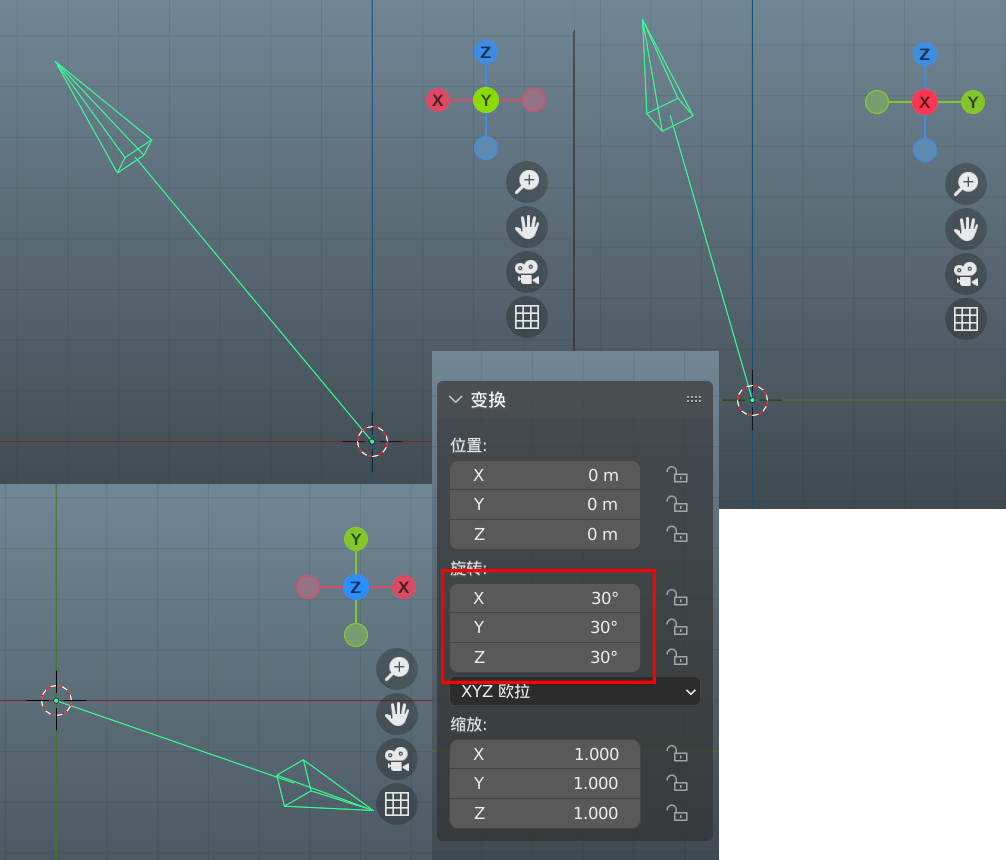
第 2 条附言 2022-02-24 00:04:12 +08:00
我目前的想法是 根据三角函数算一个直线上的点,再向量化,不知道可不可以
第 3 条附言 2022-02-24 13:58:42 +08:00
感谢大家的回复,由于只有3次附言,这是最后一次了,帖子不能再更新,有兴趣可以看回复
我的表达或许不到位,导致大家有点误解。我的最终目的是获得一个面的朝向,理由是blender的api:
bmesh.ops.bisect_plane(bm, geom=bm.faces[:] + bm.edges[:] + bm.verts[:], clear_inner=True, clear_outer=True, use_snap_center=False, plane_co=(0, 0, 0), // 这是面的中心位置 plane_no=(0, 0, 1) // 这是面的朝向 ) 面的朝向可以理解成一个法向量,也能理解成 空间中一点(x,y,z) 与原点连成的直线的法向量。或许有错误,但这里这么理解没问题。 我为了简单,转化成了直线的旋转量(没考虑到有这么多坑……),经大家的指点发现对我来说这过于复杂,没学过高数,矩阵啥的看不懂。
那就回到最开始,直接在blender里操作一个空物体,它的世界座标法向量化就是我要的。
感谢各位的帮助
此后无法更新主题,有问题回复见
1 neteroster 2022-02-23 23:10:40 +08:00 这个旋转角度是什么?好像不太清晰 |
2 kokutou 2022-02-23 23:14:49 +08:00 看看 unity 的基础教程... |
3 wudicgi 2022-02-23 23:24:53 +08:00 旋转角度分别是绕 x, y, z 轴旋转的度数吗? |
4 thedrwu 2022-02-23 23:26:03 +08:00 via Android affine transformation 注意顺序 |
5 zeronofreya OP @wudicgi 是的 |
6 zeronofreya OP @thedrwu 查了下,叫仿射变换来着,没看到相关性,我太菜了 |
7 zeronofreya OP @kokutou 这是数学相关吧? unity 难度也太高了…… |
8 zeronofreya OP @neteroster 补充了下,绕 xyz 轴旋转的角度 |
9 wudicgi 2022-02-24 00:13:10 +08:00 我没做过这方面工作,现查了一下 https://en.wikipedia.org/wiki/Rotation_matrix#Basic_rotations 这里边的 Basic rotations 是不是你需要的 比如初始的向量是 (1, 0, 0) 的话,依次乘 3 个旋转矩阵,出来的向量就是你需要的 |
10 secondwtq 2022-02-24 00:22:51 +08:00 “只知道直线的旋转角度” 这个问题本身就不明确,“旋转角度”有多种表示方式。 还好有图,楼主那个红框底下有个“XYZ Euler”,这个就是当前用的哪种旋转方式(貌似这功能我只在 Blender 上面见过) 然后再去 wiki 查就是了 |
11 wudicgi 2022-02-24 00:24:26 +08:00 好像底下 General rotations 里有 Basic rotations 中这 3 个旋转矩阵相乘的结果,直接用就可以了 注意好方向,和初始向量的值 |
12 wanglz111 2022-02-24 00:39:00 +08:00 via iPhone (cosαsinγ, sinαsinγ, cosγ) 大概类似于三重积分三角换元的思路? |
13 MCVector 2022-02-24 00:45:08 +08:00 向量乘上一个旋转矩阵就行了,如果只有旋转的话用 3x3 的旋转矩阵就可以啦。 旋转矩阵可以从旋转轴和角度构造,这个比较适合你。你也可以转化成比较通用的欧拉角和四元数。 基本上所有的图形库都可以帮你构造旋转矩阵,自己手撸的话也不复杂,就是几个正余弦函数填到相应的矩阵位置上就行了。 详情可以查你所用工具或者库的旋转矩阵构造。 |
14 MCVector 2022-02-24 00:53:42 +08:00 |
15 insraq 2022-02-24 02:06:34 +08:00 虽然我这块也不是很熟悉,但是写游戏还是用到一些。 第一个问题是 “旋转角度 (30, 30, 30)” 并不能清晰定义出一个旋转,这个取决于旋转 XYZ 轴的顺序。比如 Unity 一般是旋转 Z X Y https://docs.unity3d.com/ScriptReference/Quaternion.Euler.html 第二个问题是“方向向量”也不能清晰定义出一个旋转 - 同一个方向向量有好多种旋转方法。一般游戏中,类似问题这么处理: 用 Quaternion.Euler 拿到 Quaternion, 然后 Quaternion * Vector3.forward 拿到一个清晰定义的 Vector3 |
